[Auto] Stitching and Photo Mosaics

A.1: Shoot and Digitize Pictures

Before any coding, the first step is to take some pictures for stitching. Recall that the assumption behind image mosaicing is that the stitched images are taken from the same center of projection (COP); therefore, the quality of the final result can be significantly affected by the input images, especially when objects are close to the camera. In practice, I followed the rules below for taking photos:

1. Fix the COP and only rotate the camera, i.e., rotate about the CMOS of the camera.
2. Use a small aperture (large f-number) to ensure there is enough depth of field and (almost) everything is in focus.
3. Fix all other camera parameters, including focal length (I had to, cause my X100VI is a fixed lens camera...), ISO, S.S., and WB, which ensures that the photos have similar brightness and color and further avoids potential blending artifacts.
4. Overlap the fields of view significantly, e.g., at least $50\%$.

These rules do help me to get satisfactory mosaics in the end. We will see the results later in parts A.4 and A.5. Since the raw photos exceeded 20MB each, I resized them by a factor of 0.25 to facilitate efficient processing and visualization, which are shown below.

The first set of photos is about the T.Y.Lin Structural Engineering Demonstration Laboratory on the 5th floor of Davis Hall. In case you are not familiar with Tung-Yen Lin (林同棪), he is a Chinese-American structural engineer and Berkeley alumnus who was the pioneer of standardizing the use of prestressed concrete in building, bridges, and other structures. Stop by the lab if you are interested in learning more about his work and contributions to structural engineering.

The second set of photos is about the campus scenery from the recently built Kresge Engineering & Mathematical Sciences Library. This set contains $12$ photos in total, which have a very wide field of view, so I divided them into two groups of $6$ photos each to create two mosaics for planar image stitching at A.4, and then used all $12$ photos to create a single mosaic for cylindrical image stitching at A.5.

A.2: Recover Homographies

Before warping and stitching our images, it is necessary to recover the parameters of the homography transformation matrix $\mathbf{H} \in \mathbb{R}^{3 \times 3}$ between each pair of images, such that the new coordinate of images $\mathbf{p}' = [u,v,1]^{\top}$ (in homogeneous coordinates) can be obtained from original coordinates $\mathbf{p} = [x,y,1]^{\top}$ via linear transformation $\mathbf{p}' = \mathbf{H} \mathbf{p}$. Recall that $\mathbf{H}$ has $8$ degree of freedoms (DOFs) since the last element is a scaling factor and can be fixed to $1$, therefore, $4$ pairs of corresponding points $(\mathbf{p}',\mathbf{p})$ are sufficient to recover $\mathbf{H}$ through standard techniques.

However, in practice, recovering $\mathbf{H}$ from only $4$ pairs of corresponding points usually leads to noisy estimates, therefore, here we adopt a least-squares setting to robustly estimate $\mathbf{H}$ from $n \ge 4$ pairs of corresponding points, i.e., solving the $\mathbf{H}$ from an overdetermined linear system: $$ \mathbf{A} \mathbf{h} = \mathbf{b} ,$$ where $\mathbf{h} \in \mathbb{R}^8$ is the vectorized form of 8 DOFs of $\mathbf{H}$, $\mathbf{A} \in \mathbb{R}^{2n \times 8}$ and $\mathbf{b} \in \mathbb{R}^{2n}$ are constructed from the $n$ pairs of corresponding points.

For the derivation of such a linear system, we start from the homography transformation of a single pair of corresponding points, say, $[x,y,1]^{\top} \to [u,v,1]^{\top}$, expanded as: $$ \begin{bmatrix} \lambda u \\ \lambda v \\ \lambda \end{bmatrix} = \begin{bmatrix} h_{1} & h_{2} & h_{3} \\ h_{4} & h_{5} & h_{6} \\ h_{7} & h_{8} & 1 \end{bmatrix} \begin{bmatrix}x \\ y \\ 1 \end{bmatrix}, $$ where $\lambda$ is the scaling factor due to the introduction of homogeneous coordinates. In order to eliminate the $\lambda$ algebraically, the output vector $[\lambda u, \lambda v, \lambda]^{\top}$ can be rewritten by normalizing the first two elements with the last element, i.e., $$ \begin{aligned} u & = \frac{\lambda u}{\lambda} = (h_{1} x + h_{2} y + h_{3}) / (h_{7} x + h_{8} y + 1) \\ v &= \frac{\lambda v}{\lambda} = (h_{4} x + h_{5} y + h_{6}) / (h_{7} x + h_{8} y + 1). \end{aligned} $$ The above equations can be further rearranged to our expected linear system form: $$ \begin{matrix} h_{1} x + h_{2} y + h_{3} - u h_{7} x - u h_{8} y & = & u \\ h_{4} x + h_{5} y + h_{6} - v h_{7} x - v h_{8} y & = & v, \end{matrix} $$ which can be rewritten in matrix form as: $$ \begin{bmatrix} x & y & 1 & 0 & 0 & 0 & -ux & -uy \\ 0 & 0 & 0 & x & y & 1 & -vx & -vy \end{bmatrix} \begin{bmatrix}h_{1} \\ h_{2} \\ h_{3} \\ h_{4} \\ h_{5} \\ h_{6} \\ h_{7} \\ h_{8} \end{bmatrix} = \begin{bmatrix} u \\ v \end{bmatrix} \quad \Longrightarrow \quad \mathbf{A} \mathbf{h} = \mathbf{b}, $$ i.e., exactly the linear system we are looking for. Finally, with $n$ pairs of corresponding points, the linear system can be constructed by simply stacking the above equations vertically, i.e., $\mathbf{A} \in \mathbb{R}^{2n \times 8}$ and $\mathbf{b} \in \mathbb{R}^{2n}$. Once we have the $\mathbf{A} \mathbf{h} = \mathbf{b}$ constructed, where $n \ge 4$, solving $\mathbf{h}$ via least-squares from such an overdetermined linear system becomes trivial, i.e., with the assumption that $\text{rank}(\mathbf{A}) = 8$, the optimal solution $\mathbf{h}^{*}$ can be obtained in closed-form as: $$ \mathbf{h}^{*} = \arg\min_{\mathbf{h}} \|\mathbf{A} \mathbf{h} - \mathbf{b}\|^2_2 = \mathbf{A}^{\dagger} \mathbf{b},$$ where $\mathbf{A}^{\dagger}$ is the Moore-Penrose pseudo inverse of $\mathbf{A}$. Finally, the homography matrix $\mathbf{H}$ can be reconstructed from $\mathbf{h}^{*}$ by appending $1$ to the end of $\mathbf{h}^{*}$ and reshaping it back to a $3 \times 3$ matrix.

Demonstration

For demonstration purposes, one pair of images from the T.Y.Lin Lab photo set is used to recover the homography between source to target images. The photos and correspondences are visualized below:

A.3: Warp the Images

For applying any image transformation to warp images, including the homography we just recovered, the pixels in the output need to be filled in by sampling and interpolating from the input image; otherwise, artifacts such as holes and aliasing may occur. Therefore, here we implement inverse warping with two interpolation methods from scratch, including:

• Nearest Neighbor Interpolation: Round coordinates to the nearest pixel value, and
• Bilinear Interpolation: Use a weighted average of four neighboring pixels.

Recall that there are multiple coordinate conventions, here we follow the one that considers $(0,0)$ as the "center of the first pixel", $(0.5, 0)$ to be in between the first and second pixel, and so on, which makes our life easier when dealing with interpolation. The implemented process of warping one image to another can be roughly summarized as follows:

1. Create a rectangular canvas that tightly bounds the forward-warped corners of the source image under $\mathbf{H}$, initialized to zeros (black)
2. For each pixel in the canvas, compute its corresponding location in the input image using the inverse homography mapping
3. If the mapped location is within the source bounds, sample the source by the chosen interpolator (nearest or bilinear) and assign it to the canvas
4. Pixels that fail the bounds check remain black. We also record a binary $\alpha$ mask indicating valid samples (1) vs. invalid (0), which will be used for blending in Part A.4.

Rectification Examples

To verify our implementation and compare the difference between two interpolation methods, three rectification examples are processed and visualized below. It can be observed (if you zoom in) that bilinear interpolation produces smoother results than nearest neighbor interpolation, especially around edges and textures.

A.4: Blend the Image into a Mosaic

Once we have our warping functions ready, the final step is to warp all images with respect to a common reference view, align them properly on a large canvas, and then blend them together to create a seamless mosaic. The implementation details are as follows:

1. Choose one image as the reference view $I_r$, and compute the homography from each of the other images $I_i$ to $I_r$, denoted as $\mathbf{H}_{i \to r}$. Since I only have correspondences of adjacent image pairs, for non-adjacent image mapping, the homography can be computed by chaining the homographies of the adjacent pairs, e.g., $\mathbf{H}_{1 \to 3} = \mathbf{H}_{2 \to 3} \mathbf{H}_{1 \to 2}$. For whose mapping from right to left, the homography is simply the inverse of the left to right mapping, e.g., $\mathbf{H}_{5 \to 3} = \mathbf{H}_{3 \to 5}^{-1} = (\mathbf{H}_{4 \to 5} \mathbf{H}_{3 \to 4})^{-1}$.
2. Create a giant canvas that can fit all warped images, and initialize it to zeros (black).
3. Also initialize a canvas-sized $\alpha_{\text{canvas}}$ mask to record the mosaic region and capture the overlapping regions to the new composite image at each step for blending later.
4. Grow the mosaic from left to right sequentially:
   1. For each image $I_i$, warp it to the reference view $I_r$ using the homography $\mathbf{H}_{i\to r}$ with the warping function implemented in A.3, also take its $\alpha_i$ mask
   2. Treat each warped image as a patch, using the corresponding offsets (recorded in previous steps) to map it (together with its $\alpha_i$ mask) to the correct location on the giant canvas, i.e., its global coordinates.
   3. Before blending, use the current $\alpha_{\text{canvas}}$ and the new $\alpha_i$ to detect the overlapping region, i.e., add the new $\alpha_i$ to the existing $\alpha_{\text{canvas}}$ and find where the sum is $2$.
   4. Blend the images via weighted averaging in the overlapping region, three weights were implemented, including overlay (directly overlay the new warped image over existing mosaic, without averaging in overlapping regions), equal weights ($0.5$ weights of mosaic and new image in the overlapping region), and feathering weights (the distribution of distance to the mask border calculated by scipy.ndimage.distance_transform_edt)

Mosaic Examples and Comparison of Three Alpha Weights

Three mosaics are created and visualized here, whose source image sets are the ones introduced in A.1, including (1) T.Y.Lin Lab, (2) Campus Scenery (left), and (3) Campus Scenery (right). To show the difference between the three implemented alpha averaging weights, the T.Y.Lin Lab mosaic with each of them is presented. It is apparent that the feathering weights perform the best among the three modes, while the simple overlay produces noticeable seams, and the equal weights give wedge-like artifacts. Thanks to our efforts when taking the photos (A.1), feathering can already provide satisfactory mosaics, so there is no need to further apply other blending techniques like the Laplacian pyramid.

A.5: Bells & Whistles: Cylindrical Warping and Mosiacing

Mosaics created by homography warping work fine when the assumption of a planar scene holds and the field of view is not too wide; however, when we have a very wide field of view, e.g., over $180^{\circ}$, such mosaics usually suffer from severe distortions. To achieve better representation of ultra-wide mosaics, here we implement cylindrical projection to warp images onto a cylinder surface centered at the COP with radius of focal length $f$, and then unroll the cylinder to a flat plane for stitching.

I follow this open source lecture slides for my notation, derivation, and implementation. Suppose we have a pinhole camera with focal length $f$, for any 3D point in the world coordinate system $(X ,Y, Z)$, its projection on the image plane is recorded as $(x,y)$ with central point at $(x_c, y_c)$ (typically the center of the image). Therefore, what we have now is the photographs of the 3D world, i.e., multiple image planes with the same COP and $f$, then, what we want is to warp those image planes $I$ with points $(x,y)$ onto a cylindrical surface parameterized by $(\theta, h)$, and then unroll the cylinder to a flat plane $\tilde{I}$ with coordinates $(\tilde{x}, \tilde{y})$.

Forward Mapping

The forward mapping involves two steps:

1. Project the image plane points $(x,y)$ to the cylinder surface, i.e., $(x,y) \to (\theta, h)$, through the following equations: $$ \theta = \arctan\frac{x - x_c}{f}, \quad h = \frac{y - y_c}{\sqrt{(x - x_c)^2 + f^2}}. $$
2. Unroll the cylinder surface to a flat plane, i.e., $(\theta, h) \to (\tilde{x}, \tilde{y})$, via: $$ \tilde{x} = f \theta + \tilde{x}_c, \quad \tilde{y} = f h + \tilde{y}_c, $$ where $(\tilde{x}_c, \tilde{y}_c)$ is the central point of the unrolled cylinder image, which can simply be set to the same as $(x_c, y_c)$.

Inverse Mapping

For image warping, we need the inverse mapping, i.e., $(\tilde{x}, \tilde{y}) \to (x,y)$, which can be derived by reversing the above two steps:

1. Roll the flat plane back to the cylinder surface, i.e., $(\tilde{x}, \tilde{y}) \to (\theta, h)$, via: $$ \theta = \frac{\tilde{x} - \tilde{x}_c}{f}, \quad h = \frac{\tilde{y} - \tilde{y}_c}{f}. $$
2. Project the cylinder surface back to the image plane, i.e., $(\theta, h) \to (x,y)$, through: $$ x = f \tan\theta + x_c, \quad y = f \frac{h}{\cos\theta} + y_c. $$

Since we are projecting images onto the same cylinder surface and there is no more reference plane like previously, assume our raw images are truly taken from the same COP (at least I tried my best to follow the rules in A.1), then the alignment of cylindrically warped images can be simply done by a translation matrix rather than a full homography anymore.

With aforementioned knowledge in mind, the implementation of cylindrical warping and stitching is simply adding few more steps to the previous planar warping and stitching pipeline:

1. Define a focal length $f$ for cylindrical projection, then warp all images cylindrically using the inverse mapping derived above, which are now our "new planar images" in the unrolled cylinder coordinate system, i.e., get $\tilde{I}$ from $I$.
2. With the same cylindrical warping, get the new correspondences in the unrolled cylinder coordinate system, i.e., get $(\tilde{x}, \tilde{y})$ from $(x,y)$.
3. Instead of recovering homographies between original planar images, here we compute the translation matrices $T_{i \to r}$ in the unrolled cylinder coordinate system, i.e., finding the relative offsets of each $\tilde{I}_i$ to the reference image $\tilde{I}_r$ in the unrolled cylinder plane.
4. Then use the same approach as A.4 to put all cylindrically warped images $\tilde{I}_i$ onto a giant canvas, using the translation matrices $T_{i \to r}$ to align them properly, and blend them together.

Cylindrical Mosaic Examples

With all $5$ photos of the T.Y.Lin Lab and $12$ photos of the campus scenery, the cylindrical mosaics are created and visualized below (interpolated with bilinear method and blended with feathering technique). Compared to the planar mosaics created in A.4, it can be observed that the cylindrical mosaics have a much wider field of view (over $180^{\circ}$ for the campus scenery) and significantly reduced distortions.

B.1: Harris Corner Detection

As what we did in the manual stitching, the first step is to detect some interest points in each image such that we can find correspondences in the following steps. One of the most widely used type of point is the "corner", which is expected to have large intensity variations in all directions, therefore, it is more likely to be distinguishable from other points.

Here we implement the Harris Corner Detector for detecting our candidate interest points, which are further thresholded and suppressed for reasonable quantity and spatial distribution. The Harris matrix at Gaussian pyramid layer $l$ at pixel $(x,y)$ is computed based on its image gradients $(I_x, I_y)$ in a Gaussian window $W$ (through convolving a filter $g_{\sigma_i}$ on gradient) around it: $$ \mathbf{H}_l(x,y) = \sum_{(x,y)\in W}\begin{bmatrix} I_x^2 & I_x I_y \\ I_x I_y & I_y^2 \end{bmatrix} = \nabla_{\sigma_d}P_l(x,y) \nabla_{\sigma_d}P_l(x,y)^{\top} \star g_{\sigma_i}(x,y), $$ where $\sigma_i$ and $\sigma_d$ are the integration and gradient scales, respectively. Then, the corner strength function that quantifies how "corner-like" a pixel is defined by the harmonic mean of the eigenvalues of $\mathbf{H}$: $$ f_{HM}(x,y) = \frac{\det{\mathbf{H}_l(x,y)}}{\text{tr}{\mathbf{H}_l(x,y)}} = \frac{\lambda_1 \lambda_2}{\lambda_1 + \lambda_2}, $$ which will return high values when both eigenvalues are large, i.e., large intensity variations in both directions (implying a corner), while gives low values when at least one of the $\lambda$ is small (implying an edge or flat region). Additionally, the interested points are those local maxima of $f_{HM}$ in a small neighborhood (e.g., $5 \times 5$ window) and above a certain threshold (e.g., $0.01\max(f_{HM})$).

Adaptive Non-Maximal Suppression (ANMS)

The interested corners from Harris, even after thresholding and local maximal suppression, may still be too many and unevenly distributed, yielding unnecessary computational burden and poor stitching performance. Therefore, here we implement the Adaptive Non-Maximal Suppression (ANMS) introduced in the original paper.

Mathematically speaking, we have the interest point set $\mathcal{I}$ after Harris, whose elements all represent strong corners, and we want to get a subset of $\mathcal{I}$ such that the points are well-distributed and restricted to a certain affordable number $n_{ip}$. To achieve this, for each point $\mathbf{x}_i \in \mathcal{I}$ we compute its suppression radius $r_i$, defined as the "minimum distance to its nearest significantly stronger neighbor $j$", where the so-called "significantly stronger" is defined as $f_{HM}(i) < c_{\text{robust}} \cdot f_{HM}(j)$ (simply setting $c_{\text{robust}} = 1$ may harm robustness, therefore, we set $c_{\text{robust}} = 0.9$ as suggested in the paper). Therefore, the $r_i$ can be expressed as: $$ r_i = \min_{\mathbf{x}_j \in \mathcal{I}} |\mathbf{x}_i - \mathbf{x}_j| \quad \text{s.t.} \quad f_{HM}(i) < c_{\text{robust}} \cdot f_{HM}(j). $$ Once we have $r_i$ for all points, the desired subset can be simply obtained by sorting $r_i$ in descending order and keeping the top $n_{ip}$ points. The corner points distribution before and after ANMS are visualized below, which clearly shows that ANMS helps to select well-distributed corners across the whole image.

Examples of Harris Corner Detection before and after ANMS

One example of single-scaled Harris corner detection before and after ANMS is shown below. It can be observed that with only thresholding and selecting local maxima, the detected corners are quite dense around some texture-rich regions, while after ANMS, they are much better evenly distributed spatially.

B.2: Feature Descriptor Extraction

Once we have interested points ready, the next is to extract descriptions of local image structure, which will be further used for matching. To make the descriptions robust to subtle changes in exact feature location and illumination, here we implement the one used in the original MOPS paper with simplification. Specifically, we extract axis-aligned $8 \times 8$ patches (without rotation) for each corner that is downsampled from a $40 \times 40$ patch around the corner with equal spacing $s=5$, which is low-pass filtered before downsampling for anti-aliasing.

The implementation in the MOPS paper was approximated by directly sampling $8 \times 8$ patch one per pixel in the higher pyramid level, which is equivalent to downsampling the $40 \times 40$ patch by a factor of $5$ with blurring. Similarly, here we approximate this sampling by directly resizing the $40 \times 40$ patch to $8 \times 8$ using cv2.resize with INTER_AREA interpolation, which is approximately equivalent to the blurring and downsampling process. Finally, the $8 \times 8$ patches are normalized to zero mean and unit variance.

Examples of Extracted Feature Descriptors

Some patches ($40 \times 40$) and their corresponding $8 \times 8$ feature descriptors are shown below. One can find that the feature descriptors are able to capture the local image structure around each corner effectively without being affected by aliasing artifacts.

B.3: Feature Matching

Given the feature descriptions of a pair of images, here we implement a feature matching algorithm to find correspondences between them, hence, for any patch in one image, denoted as $I(\mathbf{x})$, we want to find its best match in the other image, denoted as $I'(\mathbf{x}')$. The matching error between two patches can be simply calculated as the squared Euclidean distance between their feature descriptors since they are normalized. Recall that the corresponding patches only appear in the overlapping region of two images, and correct matches are vital for successful stitching because least squares used for Homography recovery is very sensitive to outliers; thus, we need to implement a set of outlier rejection strategies to ensure the correctness of matches. Here we first calculate the matching errors between all pairs of patches from two images, and then roughly reject most of the outliers by applying the Lowe's strategy: instead of working on the nearest neighbor ($e_{1-NN}$), thresholding the ratio between the top two nearest neighbors ($e_{1-NN}/e_{2-NN} < t$) under the assumption that the correct matches should always have substantially lower error than incorrect matches.

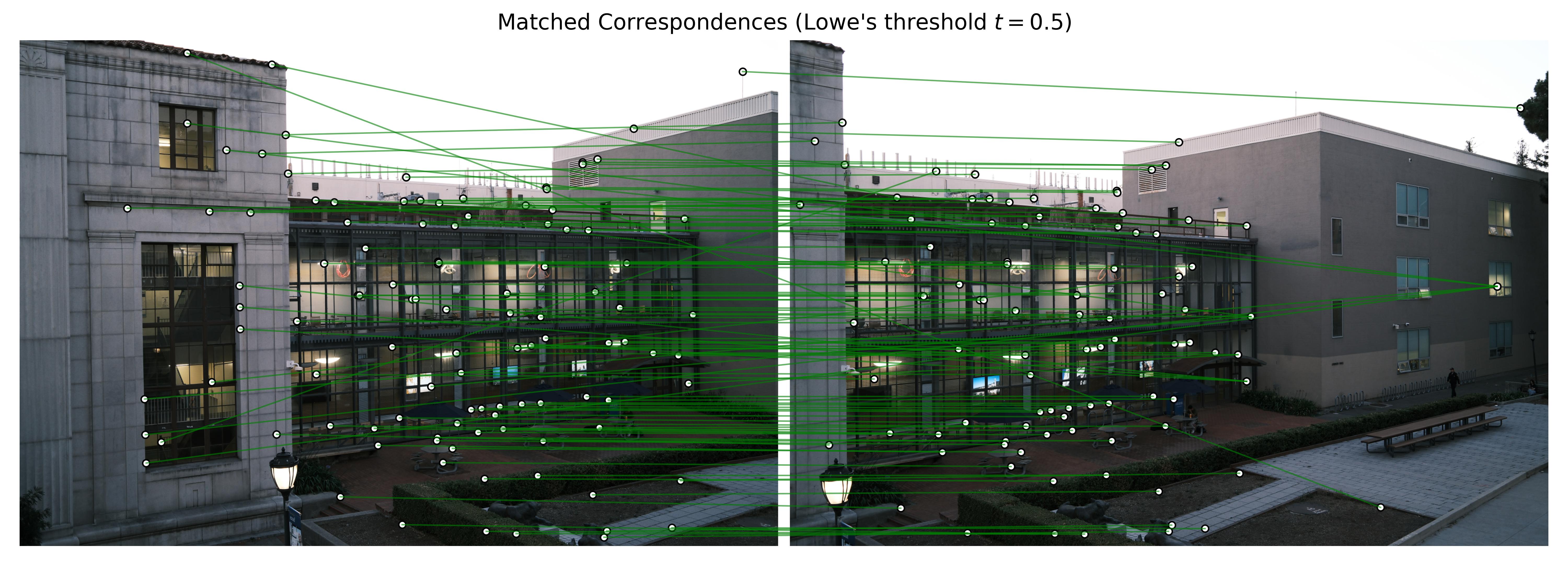
Examples of Feature Matching Results

Some matching results are shown below. It is obvious that most of the points that do not have a correct match (e.g., those in non-overlapped regions, or corners not detected in the other image) are effectively removed thanks to Lowe's strategy. However, unless the Lowe's threshold is set properly, there may still be some outliers present, which can be further removed by applying RANSAC later.

B.4: RANSAC for Robust Homography

Lowe's strategy rejects most of the outliers, however, there may still be some outliers left that can significantly harm the homography recovery, hence, here we implement the Random Sample Consensus (RANSAC) algorithm to further robustly reject all outliers left. The RANSAC algorithm follows an iterative process:

1. Randomly select the minimum number of points for estimating the model ($4$ for homography)
2. Fit the model with the selected points, i.e., compute the homography
3. Compute inliers by thresholding the error of all points with respect to the fitted model, here is $\|\mathbf{x}' - \mathbf{Hx}\| < \epsilon$
4. Repeat the above 3 steps for $N$ iterations, and keep the most inliers
5. Refit the model with all inliers for the final result

After applying RANSAC, we can obtain a robust homography matrix, which are further utilized for image stitching.

Examples of RANSAC Results

The matched correspondences shown in B.3 are further refined by RANSAC and shown below. Apparently, those inliers are more consistent and reliable for estimating the homography, while all outliers are effectively kicked out.

Mosaics with Single-scale Automatic Stitching

With all aforementioned techniques, the homographies recovered from the inliers can be utilized to create mosaics with the same pipeline introduced in Part A. The same set of images as used in the previous manually stitched mosaics is used here for comparison purposes. Compared with the manually stitched mosaics (the first one of each pair), the automatically stitched mosaics (the second one of each pair) demonstrate almost the same visual quality, implying the effectiveness of implemented techniques.

B.5: Bells & Whistles: Multi-Scale Processing

The auto stitching pipeline implemented above works reasonably well after carefully tuning those hyperparameters. Here, we further improve its robustness and stitching quality by extending to a multi-scale framework. The main idea behind multi-scale processing is that the Harris detector is non-invariant to image scale, which means we are potentially missing some good corners. The implementation of such multi-scale processing is straightforward, built upon the existing single-scale version. My implementation details are as follows:

Multi-Scale Harris Corner Detection

1. Create a Gaussian pyramid for the input image
2. Apply the Harris corner detection (with thresholding and ANMS) at each layer $l$ to get corners at different scales, record local layer coordinates, say $\mathbf{x}_{i}^{(l)} = (x_l, y_l)$ is the coordinate of corner $i$ detected at layer $l$ in that layer
3. Collect all corners from different layers, then map all corners back to the original image coordinate system (the $l_0$ layer), therefore, $\mathbf{x}_{i}^{(l0)} = (2^l x_l, 2^l y_l)$ is the coordinate of corner $i$ from layer $l$ at the $l_0$ layer
4. Apply ANMS on all collected corners in step $3$ in the $l_0$ coordinate system, keeping the top $n_{ip}$ corners as final output. At this step, each corner contains the information of: (a) which layer $l$ it is detected from, (b) its coordinate in its local layer $\mathbf{x}_{i}^{(l)} = (x_l, y_l)$, (c) its coordinate in the $l_0$ image $\mathbf{x}_{i}^{(l0)} = (2^l x_l, 2^l y_l)$

The comparison between single-scale and multi-scale corner detection is shown below; one can find that most of the corners are the same across them, which implies why the single-scale version can work well, as demonstrated before. Meanwhile, there are some differences between single- and multi-scale versions, meaning that the multi-scale version can potentially detect more corners at different scales, giving better results.

Multi-Scale Feature Descriptor Extraction

Extending the feature descriptor to multi-scale is simple, since we recorded which layer each corner is detected from and its local layer coordinate $\mathbf{x}_{i}^{(l)} = (x_l, y_l)$ in the multi-scale Harris corner detection step, here we can simply apply the single-scale feature descriptor of each corner at its corresponding layer and local coordinate. Then, we again have $8 \times 8$ normalized patches as feature descriptors for all corners across multiple scales.

The following figure illustrates the patches extracted from different layers and mapped back to the original image coordinate system. Corners from higher layers have a larger field of view to get their features.

Mosaics with Single-Scale Automatic Stitching

The rest steps to create the automatically stitched mosaics with multi-scale processing are exactly the same as the single-scale version. The mosaics of the same sets of images created by multi-scale processing are shown below. It can be observed that they are visually similar to our previous manually stitched mosaics, as well as single-scale automatically stitched mosaics (at least I can not distinguish them and say which is better), meaning that our system is well developed and robust for such three sets of photos at hand.